Where Beauty Meets Math: The Concinnitas Series

Gallery view of the Concinnitas equations on view in Picturing Math: Selections from the Department of Drawings and Prints

«The exhibition Picturing Math: Selections from the Department of Drawings and Prints, on view in gallery 690 through May 8, is anchored by a group of 10 aquatints depicting mathematical equations published in 2014 under the title Concinnitas. This title originates from Leon Battista Alberti's treatise on architecture (De Re Aedificatoria), where it is used to describe a form of beauty derived from harmony in numbers and proportion. This concept encapsulates the ideal behind the print series, which began with a chance meeting between Daniel Rockmore (Department of Mathematics, Dartmouth College) and Bob Feldman (Parasol Press, Ltd.) and the ensuing discussion about the parallels between the practice of art and mathematics.»

Their shared enthusiasm led them to invite 10 prominent mathematicians and physicists to select what they considered to be "the most beautiful or elegant mathematical expression." The 10 equations chosen for the Concinnitas portfolio were then printed as aquatints, reminiscent of chalk on a blackboard, and are accompanied by brief expository essays intended to explicate the selection process, and to comment on the significance of beauty as a motivational force in the production of mathematics.[1]

Included below are selected quotations from the essays accompanying the equations chosen by each mathematician. (The entire essay by each mathematician is available in the gallery as well.) Individually the texts shed light on how the mathematicians conceive of their profession and situate the practice and production of mathematics within a broader social and cultural sphere. Collectively they highlight some of the overall themes of Picturing Math—namely the relations between art and science; the myriad ways that information may be visualized; the nature of beauty, as conceived by mathematicians; the role of happenstance in the production of knowledge; and the years of labor and hard work hidden behind the established aesthetic of the equation scrawled onto a blackboard.

This pairing of text and images is meant to open up additional avenues for the consideration of the concept of beauty and its relationship to mathematics. It may be that beauty meets math at its moment of abstraction: one is able to recognize beauty despite the imminent difficulty of achieving it (its recognizability is part of what defines it). In this instance, the equations offer themselves for lay assessment firstly according to their aesthetic qualities. Beauty, itself an unstable epistemological entity with its own fraught and conflicted history, is sited here in the exquisite abstraction that emerges from the forging of the gestural line with a symbolic, technical language. Yet even as higher-level math is "celebrated for its insularity from the mundane and messy facts of the physical world,"[2] the companion texts hint at the latent desires, cultural aspirations, pedagogical contexts, and personal histories lying furtively beneath the surface of these groundbreaking, if not iconic, equations.

Sir Michael Atiyah: "The Index Theorem"

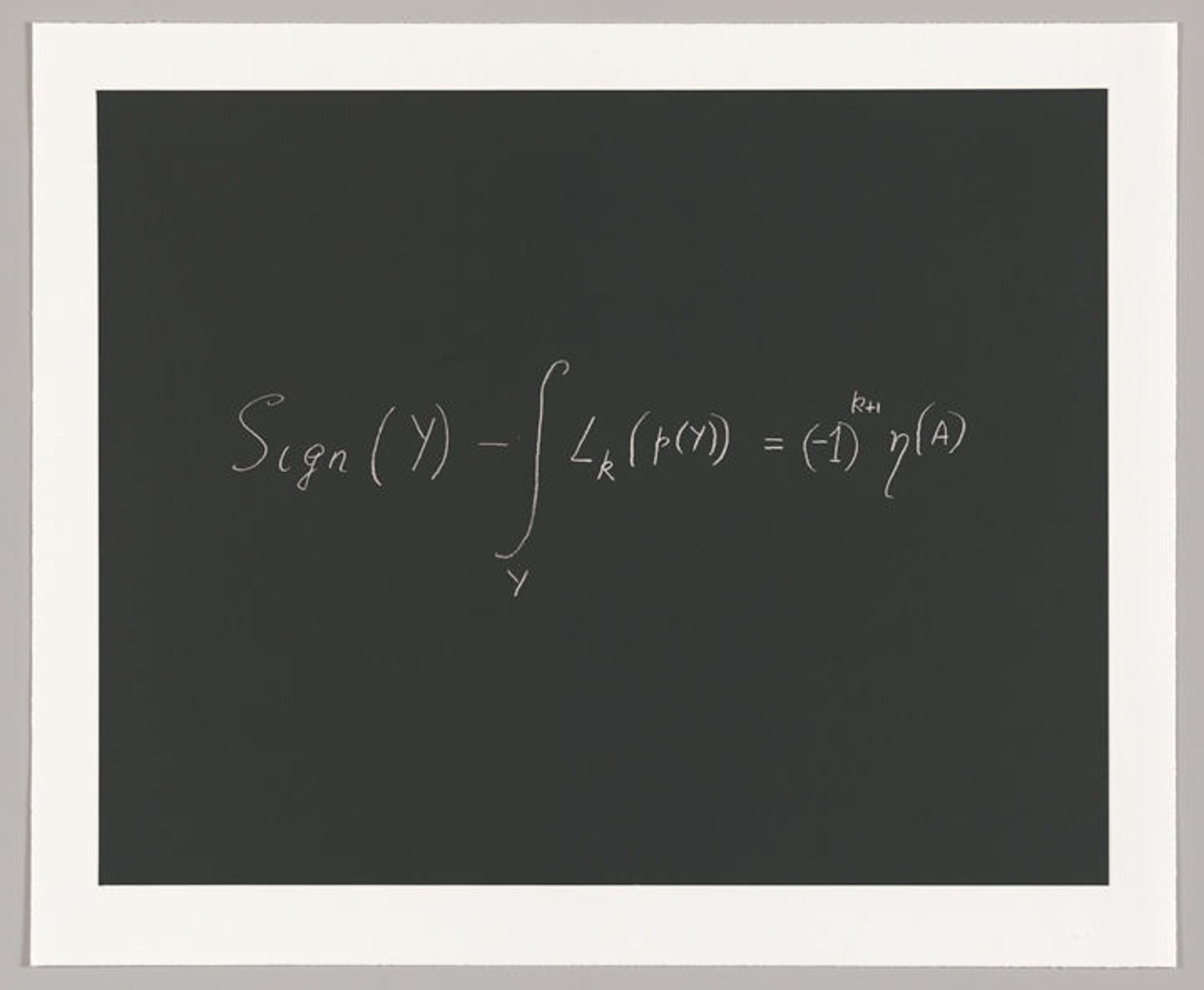
Sir Michael Atiyah (British, born 1929). Concinnitas, 2014. Printed by Harlan & Weaver, Inc.; published by Parasol Press Ltd. Aquatint, Plate: 22 x 30 in. (55.9 x 76.2 cm); Sheet: 26 1/8 x 31 5/8 in. (66.4 x 80.3 cm). The Metropolitan Museum of Art, New York, John B. Turner Fund, 2015 (2015.518)

"Mathematics is both an Art and a Science and beauty plays an essential role, a fact recognized by all mathematicians. The great German mathematician Hermann Weyl, one of my heroes, put it well when he said: 'My work has always tried to unite the true with the beautiful and when I had to choose one or the other I usually chose the beautiful.'"

Enrico Bombieri: "The Ree Group Formula"

Enrico Bombieri (Italian, born 1940). Concinnitas, 2014

"Does beauty exist in mathematics? The question concerns mathematical objects and their relations, the real subject of verifiable proofs. Mathematicians generally agree that beauty does exist in the structural beauty of theorems and proofs, even if most of the time it is largely visible only to mathematicians themselves."

Simon Donaldson: "Ampère's Law"

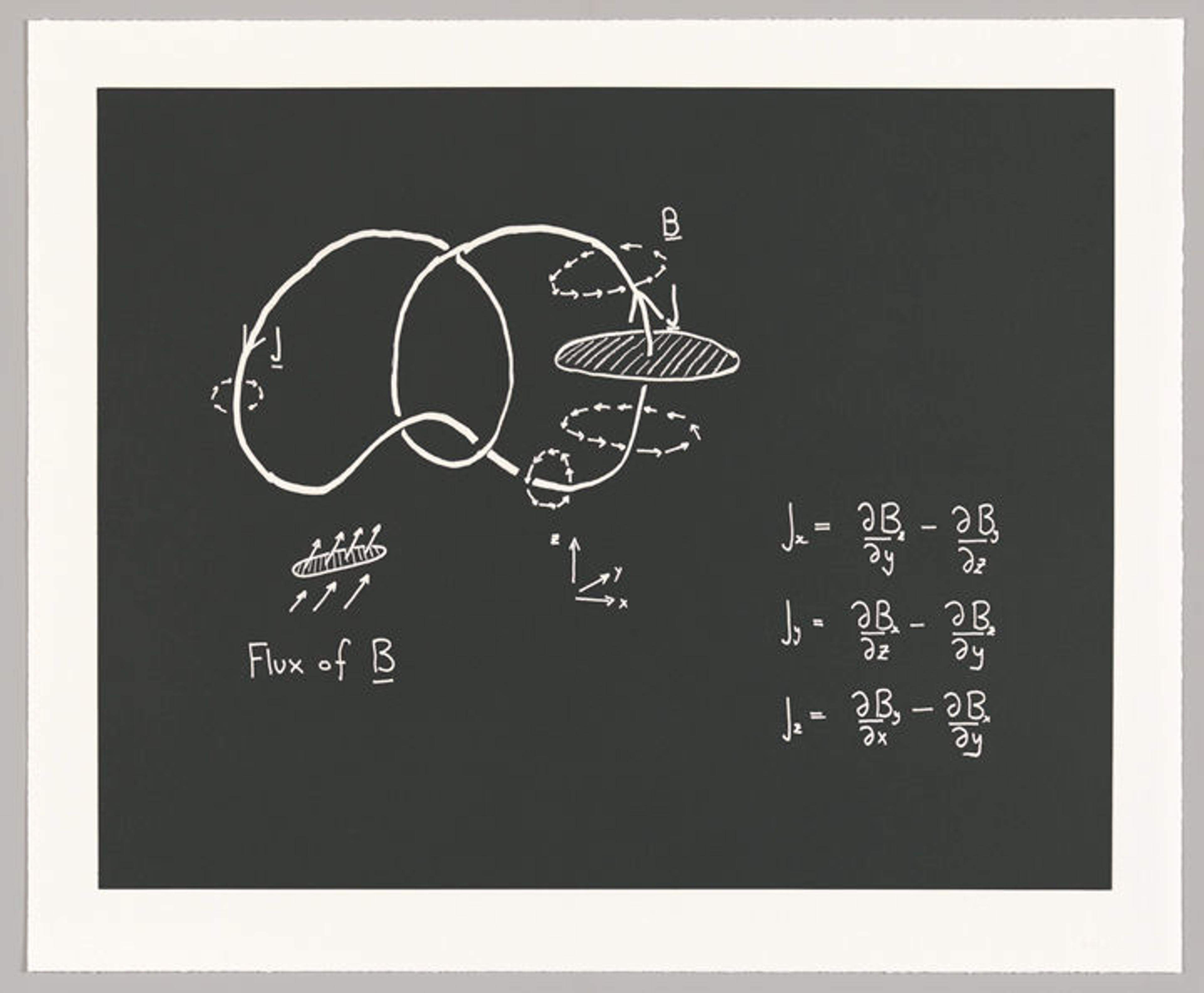
Simon Donaldson (British, born 1957). Concinnitas, 2014

"This board attempts to convey, or at least hint at, several broad aspects of mathematics which I find beautiful. On the left we see a picture and words: in the lower right, a set of equations. These are different descriptions of the same thing and they stimulate different ways of thought: pictorial and symbolic."

Freeman Dyson: "The MacDonald Equation"

Freeman Dyson (American, born Crowthorne, England, 1923). Concinnitas, 2014

"The MacDonald Equation is the most beautiful thing that I ever discovered. It belongs to the theory of numbers, the most useless and ancient branch of mathematics. My friend Ian MacDonald had the joy of discovering it first, and I had the almost equal joy of discovering it second. Neither of us knew that the other was working on it. We had daughters in the same class at school, so we talked about our daughters and not about mathematics."

Richard M. Karp: "P Versus NP"

Richard M. Karp (American, born 1935). Concinnitas, 2014

"Beauty in mathematics can be found at many levels: in the symmetry and elegance of mathematical curves, surfaces and combinatorial structures; in the subtle logic of mathematical proofs; or, as in the case of NP-completeness, in the discovery that a large number of seemingly unrelated mathematical phenomena are all manifestations of a single underlying principle."

David Bryant Mumford: "Thirteen??"

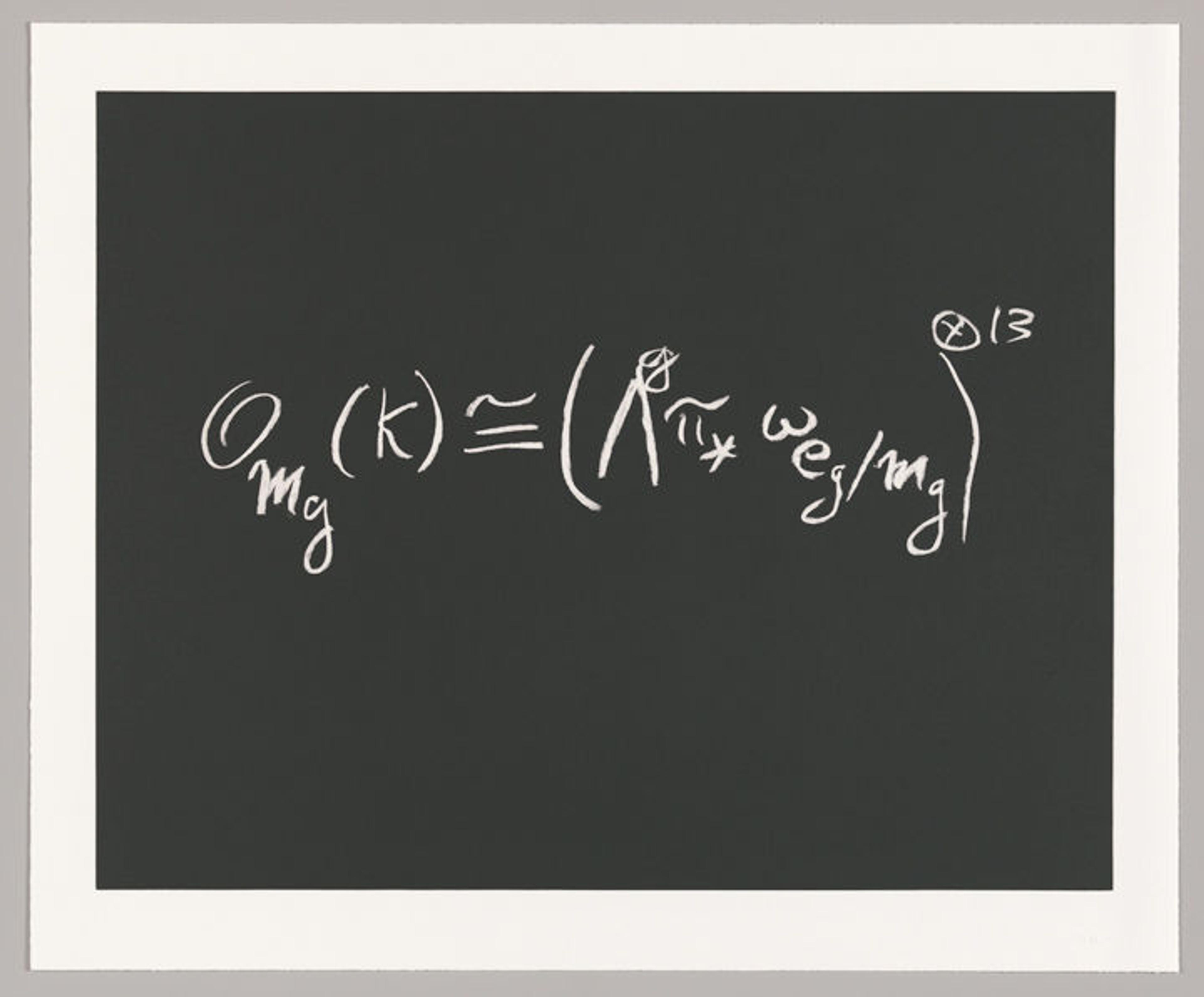
David Bryant Mumford (American, born 1937). Concinnitas, 2014

"A large part of what a mathematician does may be described as exploring 'things' which they discover through reasoning, which become as real to them as the house they live in but which have no material existence at all."

Murray Gell-Mann: "'Color': SU3 Symmetry Group Exactly Conserved"

Murray Gell-Mann (American, born 1929). Concinnitas, 2014

"I recall that in arriving, along with some colleagues, at this formulation, it came not as a burst of intuition, but rather as an accretion of steady work, and this expression summarizes not just a truth about the world, but a lot of hard work over a long period of time, each term 'plucked' from a body of discoveries over a number of years."

Peter Lax: "Conservation Laws"

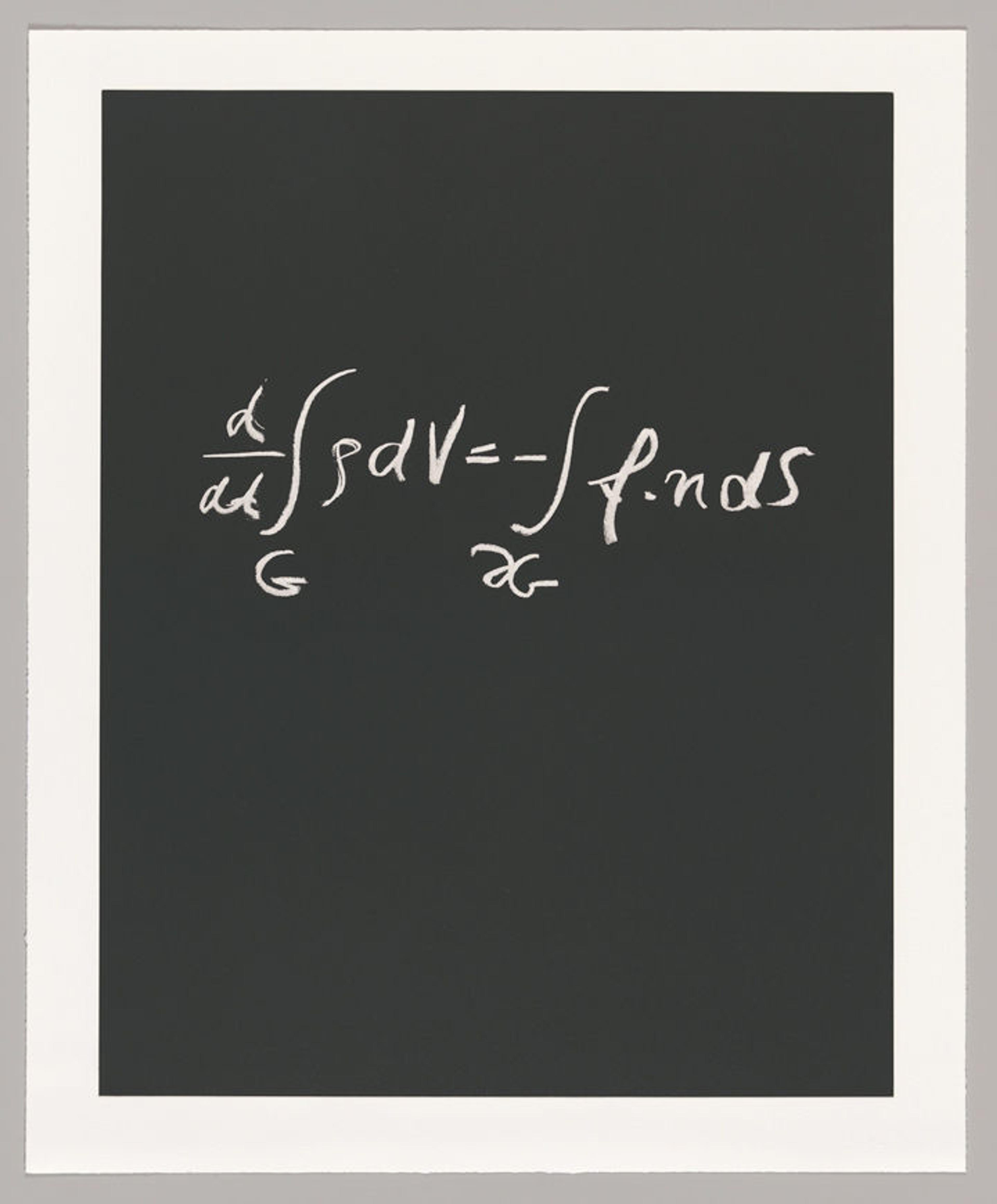
Peter Lax (American, born Budapest, 1926). Concinnitas, 2014

"A conservation law says that the total amount of some quantity, like mass, momentum or energy contained in any domain, changes at the rate at which this quantity flows across or is created at the boundary of the domain. I find this idea beautiful because it is so basic. But once you specify details of the rate of creation you get a huge variety of phenomena."

Stephen Smale: "Newton's Method"

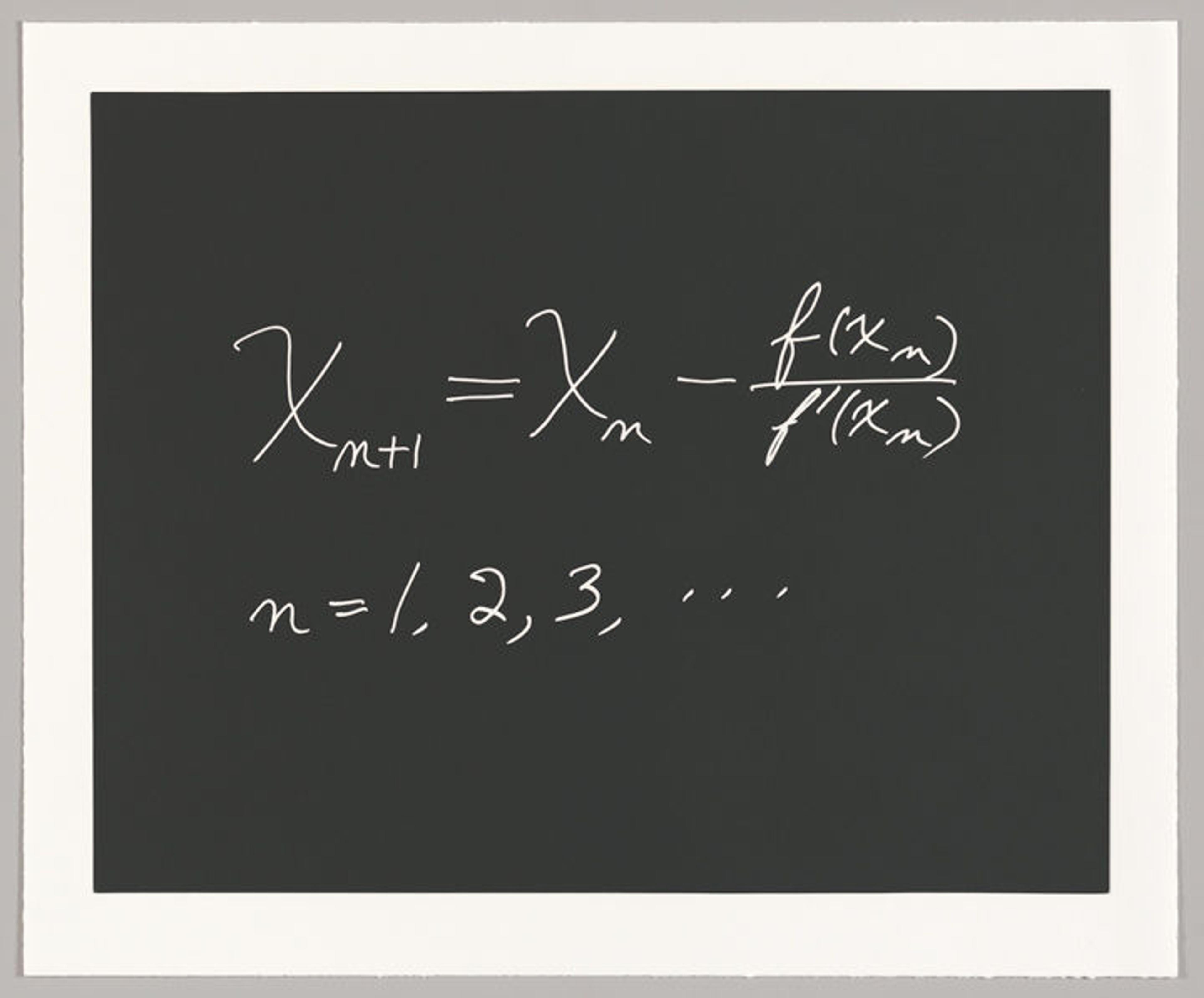
Stephen Smale (American, born 1930). Concinnitas, 2014

"John Keats has written, 'Beauty is truth, truth beauty." He has also written, 'A thing of beauty is a joy forever.' I wish to add, 'Beauty is simple and it is profound.'"

Steven Weinberg: "The Lagrangian of the Electroweak Theory"

Steven Weinberg (American, born 1933). Concinnitas, 2014

"This equation may not look beautiful. Its beauty lies in its rigidity—once its ingredients are specified, its structure is pretty well fixed by conditions of mathematical consistency. Leave out one line, or just change a minus sign to a plus sign and the whole thing would become inconsistent."

Editor's Note: Portions of this article's content were updated on April 26, 2017.

Footnotes
[1] The concept of concinnitas originates in Roman theories of oration and was later adopted by Leon Battista Alberti in order to describe the nature and methods of achieving architectural beauty. Aware of beauty's elusiveness, Alberti's concinnitas did not specify exact architectural components and, much like Cicero's rhetoric, adhered to what he described as the gestural elements of architecture. Concinnitas was considered by 19th- and 20th-century art historians, most notably Jacob Burckhardt, as "the most expressive" of Alberti's concepts. The author wishes to thank Nimrod Reitman for his insight on Alberti.

[2] Christopher J. Phillips, The New Math: A Political History (Chicago and London: University of Chicago Press), 5.

Related Link
Picturing Math: Selections from the Department of Drawings and Prints, on view at The Met Fifth Avenue through May 8, 2017